本节书摘来自华章计算机《编写高质量代码：改善c程序代码的125个建议》一书中的第3章，建议18-3,作者：马　伟 更多章节内容可以访问云栖社区“华章计算机”公众号查看。

建议18-3：避免浮点变量用“==”或“!=”与0进行比较

其实，关于浮点数的比较，早在建议3-4中就做了比较详细的介绍，本节将继续向大家做一些实用性的讲解。

我们知道，在C语言中，无论是float 还是double 浮点数类型的变量，都有其精度的限制。对于超出精度限制的浮点数，计算机会把它们的精度之外的小数部分截断。因此，原本就不相等的两个浮点数在计算机中就可能变成相等的，如下面的示例代码所示：

int main (void){    float a=10.22222225;    float b=10.22222229;    if (a == b )    {            printf("a==b \n");    }    else    {            printf("a!=b\n");    }    return 0;}

在上面的代码中，从数学上讲，a和b是不相等的，但是在32位计算机中它们却是相等的，因此程序的输出结果为“a==b”。由此可见，我们一定要避免将浮点类型的变量直接用“==”或“！=”与数字进行比较，而应该设法把它们转化成“>”或“<=”的形式。

如果两个同符号的浮点数之差的绝对值小于或等于某一个可接受的误差EPSILON（即精度），就认为它们是相等的，否则就是不相等的。两个浮点数x与y是否相等的正确的比较方式如下面的代码所示：

if( fabs(x-y) <= EPSILON )        // x等于yif( fabs(x-y) > EPSILON )         // x不等于y

同理，浮点数x和0是否相等的正确比较方式如下面的代码所示：

if( fabs(x) <= EPSILON )          // x等于0if( fabs(x) > EPSILON )           // x不等于0

下面，为了加深大家的理解，我们来看一个完整的例子，如代码清单3-1所示。

代码清单3-1　浮点数比较示例#include 
    
     #include 
     
      #define EPSILON 0.000000001int main (void){    double a = 10.22222225;    double b = 10.22222222;    double c = 0.0000001;    if ( fabs(a-b) <= EPSILON )    {            printf("a:%.12f == b:%2.12f,                         精度为%.12f \n",a,b,EPSILON);    }    else    {            printf("a:%.12f != b:%2.12f,                        精度为%.12f \n",a,b,EPSILON);    }    if (fabs(c) <= EPSILON)    {            printf("c:%.12f == 0, 精度为%.12f \n",c,EPSILON);    }    else    {            printf("c:%.12f != 0, 精度为%.12f \n",c, EPSILON);    }    return 0;}
     
    

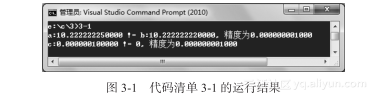
代码清单3-1的运行结果如图3-1所示。